Egy nagyon kedves ismerősömmel beszélgetve jött fel ismét a téma: a nagy tömbökből kimaradó politikai erők csak megosztják a rendszerellenes szavazatokat, ezért nem kívánatosak az ellenzék számára, már a létezésük is ártalmas. Túl azon az érzelmi töltetű káron, szomorúságon, amit ez a megállapítás egy ilyen relációban tud okozni, sajnos a széles közvélemény előtt ugyanez a megállapítás sokkal ártalmasabb. Folyományaként ugyanis a nagy tömbökből kimaradó, és ezért a valódi közügyekben – mint például Budapest sorsa – elvileg mindkét oldallal kooperációra alkalmas független szereplők végül mindkét tömb számára szalonképtelenek, megvetés és kiszorítás tárgyai lesznek. Hiszen bárhonnan nézzük is, az ilyen mindig a másik szekerét tolja.

Összefogás – szükségszerű?
(Az eredeti innen)
A tömbök, a szekértolás, a remények és a reménytelenség
A mostani vizsgálatot szubjektív – de szigorúan véve semennyire sem tudományos – módon kiválóan alátámasztja, hogy a Sétáló Budapest aktivistái között saját magamon kívül nemigen találkoztam olyannal, aki Puzsér hiányában Karácsony Gergelyre szavazott volna. A többiek tehát alátámasztották az én elméletemet az ellenzékmegosztás hamis voltáról, miközben én magam voltam az ellenpélda.
Az én gondolatmenetem egyébként ezen a téren az volt, hogy még ha Karácsony Gergely nem a legjobb főpolgármester-jelölt is, legalább nem fogja például a Rákóczi úti villamost úgy elépíteni, mint ahogy Tarlós István tervezi. Végül tényleg nem úgy építette el, csak finomabban – finomabb elépítés azonban körülbelül annyira létezik, mint a másodlagos frissességű tokhal. Azt is reméltem, hogy egy Karácsony-ciklusban lesz esélye a pesti rakpartnak és az útdíjnak is. Nem lett.
Szóval, a mai tudásommal már azt se bánnám, ha a főpolgármesteri választáson az ellenzéket „osztottuk volna meg”. Ebben a „nem annyira gáz” versenyben Tarlós utólag felzárkózott. Pedig igazán öldöklő verseny volt!
A tágabb politikai kontextussal eleget foglalkoztunk, és fogunk is még foglalkozni (kell is, hiszen a téveszmék csak a nagy tömbök sérthetetlenségét szolgálják), ezért most a XI. kerületi 2019-es önkormányzati választások eredményének rövid elemzésével csak annyit mutatunk meg, hogy e körben az „ellenzékmegosztós” hipotézis jó eséllyel nem volt igaz. (Egy érdekesség ebben a témában, hogy a G7.hu 2019-ben már forró nyomon elemezte a XII. kerületet, és ott nem is csak a cáfolatig, hanem egyenesen ellentétes eredményre jutott.)
A kérdésünk az, hogy a XI. kerületben a Sétáló Budapest-szavazói mintázatok mire hasonlítanak jobban. Ha az ellenzékére, akkor minden alapunk megvan arra gondolni, hogy az ellenzékhez hasonló helyről jövő, tehát hasonló helyzetű, hasonló társadalmi státuszú, feltehetőleg inkább hasonlóan mint különbözően gondolkodó emberek, azaz a potenciális ellenzéki szavazók szavaztak a Sétáló Budapest jelöltjeire. Ekkor teljesül, hogy a Sétáló Budapest megosztotta az ellenzék hitbizománynak tekintett táborát, és noha senki sem tilthatja meg neki, hogy hitelesebb próbáljon lenni, vagy a NER-t a saját ellenzékével leváltó „rendszerváltásnál” messzebbre próbáljon tekinteni, technikai értelemben valóban csak hátráltatja a Fidesz-kormányzás végét. Ezzel ellentétben, ha a mintázatok a Fideszéire hasonlítanak, elég erős bökkenő van a kiszorítósdiban: a Sétáló Budapest nem indulása még technikai értelemben is csak a Fideszt segíti.
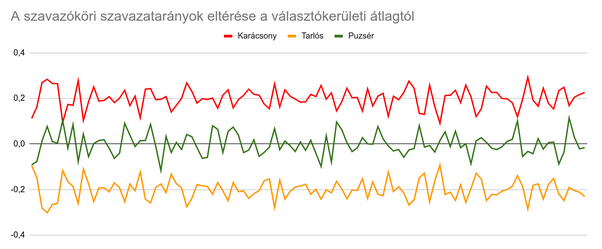
Először egy képszerű összehasonlítás: melyik „nagy játékoséra” hasonlít a Sétáló Budapest adatsora (zöld)? Az ábra szépsége és olvashatósága kedvéért a baloldali jelölt adatsorát (piros) 0,2-vel felfelé, a Fideszét (narancs) 0,2-vel lefelé toltuk el, a Sétáló Budapestét pedig a kb. tizednyi szavazatarány és a kb. dupla relatív szórás fényében ötszörösére növeltük. A vízszintes tengelyen az egyes szavazókörök vannak (jelölés nélkül)
Az adatsorok számszerű összehasonlítását lineáris illesztéssel fogjuk végezni, a főpolgármesterre leadott szavazatok körén belül megpróbáljuk előállítani a Puzsér Róbertre leadott szavazatok adatsorát a Karácsony Gergelyre leadott szavazatok és a Tarlós Istvánra leadott szavazatok lineáris kombinációjaként (erről lásd a keretest, de aki nem kíváncsi rá, olvassa úgy, hogy „keverékeként”). Nem pontosan állítható elő a Puzsér-adatsor a másik kettőből (Miért is lehetne? Ezért végzünk csak egy illesztést.), de előállítható a Puzsér-szavazatok adatsorának egy legjobb (legkevésbé rossz) közelítése. E legjobb közelítés lesz a másik két adatsornak egy olyan keveréke, amiben érdemes megnézni, hogy végül melyik mekkora súllyal szerepelt, melyik dominálja a keveréket, azaz melyik hasonlít rá jobban.
Vetítsünk: a legkisebb négyzetek módszere, lineáris regresszió
Hogy most se maradjunk tudományos ismeretterjesztés nélkül, röviden nézzük meg, hogyan közelítjük a Puzsér-adatsort a másik kettő lineáris kombinációjaként, azaz egy-egy konstans szorzóval alkotott súlyozott összegeként! (Ez a „lineáris regresszió” néven ismert algoritmuscsalád egy egyszerű tagja lesz.)
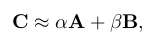
azaz
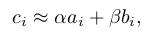
ahol i jelöli az egyes szavazóköröket, és ha N darab szavazókör van, akkor A, B, C nem mások, mint az ai, bi, ci számokból alkotott N elemű felsorolások, azaz vektorok.
De miért is neveztem az N elemű számsorokat vektoroknak? Ha csak három szavazókör volna, akkor a háromdimenziós tér vekoraival nagyon jól tudnánk szemléltetni nemcsak ezt, hanem az egész gondolatmenetet.
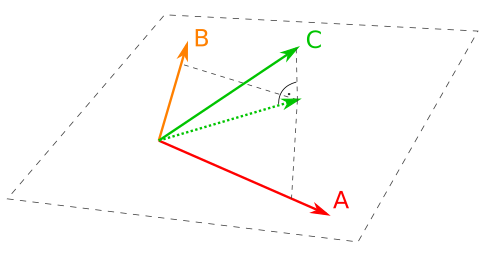
A C vektor vetítése az A és B által kifeszített síkra. A C vetített képe előáll az A és B vektorok valahányszorosának összegeként (azaz lineáris kombinációjaként); ez a C legjobb közelítése a síkon belül
Három szavazókör esetében a háromelemű szavazatszám-listák értelmezhetőek úgy, mint vektorok koordinátái, és ha ezeket felrajzoljuk a térben, akkor kiválóan látszik az is, mit csinálunk akkor, amikor az egyiket a másik kettő lineáris kombinációjaként közelítjük: a közelítendő vektort rávetítjük a másik kettő által kifeszített síkra. A sík ugyanis nem más, mint az őt kifeszítő vektorok összes lineáris kombinációját tartalmazó tartomány, ezen belül pedig a C legjobb közelítése az erre a síkra merőlegesen vetített kép.
Azok pedig, akik egy kicsit még emlékeznek a koordinátageometriára, a C és az őt közelítő keverékvektor (végpontjainak) távolságát is fel tudják írni:
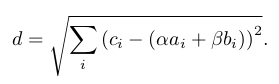
Ez a távolság két paramétertől (α-tól és β-tól) függ, s e két paraméter optimális értéke akkor áll elő, amikor a tőlük függő d(α,β) minimális. Ennek levezetésétől már eltekintünk, de a lényeg a fontos: ha nem három, hanem tetszőleges N számú szavazókör, azaz adatsor-elem van, az eljárás ugyanúgy működik, és ugyanúgy egy merőleges vetítésként értelmezhető (ugyanúgy C-t az A és B síkjára), csak nem a háromdimenziós, hanem az N dimenziós térben.
Ha a valószínűségszámítással és statisztikával foglalkozó emberek az adatsorokat valószínűségi változóként értelmezik, és az elméleti eloszlásukat ismerik vagy ismerni vélik, a vetítés során előálló távolsági adatokat mindenféle valószínűségi értelmezéssé is át tudják alakítani. Ezek után alakulnak az alkalmazott közelítés pontatlanságai „magyarázó erővé” és hasonlókká a politikai elemzők nyelvén, de ennek tárgyalásától most még inkább eltekintünk.
Az illesztés során nem pontosan a szavazóköri szavazatszámokat dolgozzuk fel, hanem a szavazati arányokat, illetve azoknak is az egyéni képviselői választókerület átlagától való eltéréseit. Ez az előkészítés most csak egy heurisztikus döntés alapján van így, éspedig azért, mert az egyes választókerületek között a hármas politikai versenyt lényegében véletlenszerűen befolyásoló, nem tendenciózus különbségek vannak (legfőképpen az, hogy az adott kerületben a Sétáló Budapest tudott-e képviselőjelöltet indítani, de például az is, hogy éppen melyik párt reprezentálta helyben az összefogást). Ezek a választókerületek közötti fluktuációk sokkal inkább „zajt”, mint „adatot” jelentenek, és ezért az illesztést nem érdemes azzal terhelni, hogy Puzsér-adatsorban ezeket a hatásokat is megpróbálja az algoritmus a másik kettőből kikeverni. Egy komolyabb vizsgálatban biztos, hogy ennél alaposabb előkészítésre is futná, de a mi gyors elemzésünkhoz ez már legyen így jó.
Az illesztésből ki kellett venni továbbá a legjobban teljesítő jelöltünk – innen is gratulálunk neki, hiszen nagyjából dupla annyi szavazatot kampányolt össze, mint a többiek! – választókerületét is, mivel az ő kirobbanó eredményei elég hektikus, valószínűleg az egyes szavazókörökben meglevő ismertségét, intenzív kampánytevékenységét tükröző mintázatot mutattak. Ennek reménytelen lekövetésével, kikeverésével sem érdemes terhelni az illesztést. Itt jegyezzük azonban meg, hogy még az adatsorok legesetlegesebb fluktuációi is lehetnének egymásból magyarázhatóak, ha tényleg létezne valami nagyon szoros átjárási kapcsolat a Sétáló Budapest szavazói és valamelyik nagy tömbé között. Az, hogy ilyen nem figyelhető meg (azaz az egész heurisztikus előkészítés szükségessége, vagy legalábbis szükségességének látszata), előre sejteti, hogy szoros kapcsolatot egyik irányban sem fogunk tudni kimutatni.
Maradnak tehát vizsgálatunkban a képviselői egyéni választókerületeken belüli mintázatok, amelyek meglehetősen homogén választási versenyben születtek, és így valószínűsíthető, hogy ezeken belül a választók részhalmazokra osztásából eredő eredménykülönbségek nagyrészt az alapvető egyéni választói preferenciák részhalmazonkénti tendenciaszerű eltéréséből erednek. (Ezek pedig azért térhetnek el tendenciaszerűen, mert egy-egy szavazókör társadalmilag homogénebb lehet, mint az egész választókerület. Például az egyik szavazókör jómódúbb környék, mint a másik, az egyik társasházas, a másik családi házas, az egyik jobbára fiatalabb szavazókat tartalmaz, mint a másik, stb.)
Az eredmény
(Ezt a címet azért tettem ide, hogy könnyű legyen átugorni az idáig hömpölygő módszertani felvezetést. Aki tényleg-tényleg csak a végkövetkeztetésre kíváncsi, ugorjon még lejjebb, a „Tényleg az eredmény”-re!)
Az eredmény végül az, hogy a legjobb választókerületünktől megfosztott szavazatszám-adatsorok 109 dimenziós terében az egyes jelöltek adatsorai körülbelül úgy helyezkednek el, ahogy a keretes módszertani szöveg ábráján látható, csak a zöld nyíl, a Puzsér-adatsor az ott lerajzolttal ellentétes irányba mutat: a negatív keverési együtthatók révén a másik két adatsor által meghatározott tompaszög (kb. 167°) „külső” oldalára kerül.
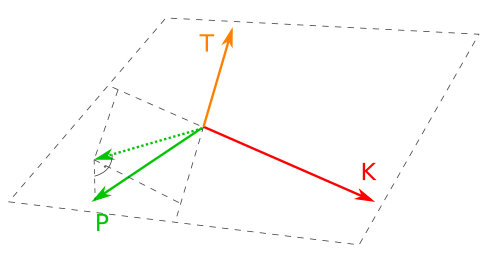
A szavazati adatsorvektorok így helyezkednek el. A P a sík alatt van, a többi a síkban; P pontozott közelítése (vetítése) egy kicsit kisebb szöget zár be T-vel, mint K-val.
A síkon belül, a tompaszöget alkotó Karácsony- és Tarlós-vektorok között nagyjából félúton, de egy kicsit a Tarlós-vektorhoz (hat és fél fokkal) közelebb helyezkedik el a Puzsér-adatsort közelítő Karácsony–Tarlós-keverék. Ehhez képest az igazi Puzsér-adatsor kb. 20 fokkal tér el, azaz ennyivel emelkedik ki a másik két adatsor által kifeszített síkból. (Ínyencebbeknek: a Puzsér-adatsor másik kettőtől teljesen független fluktuációja számottevően nagyobb, mint a két tömb felé kimutatható aszimmetria erőssége, ezért az aszimmetria nem mondható jelentősnek.)
Most jut az eszembe
Ha azt akarjuk tesztelni, hogy a „nagyok” közül kihez áll közelebb a Puzsér-szavazatok mintázata, akkor egyszerűen képezhetjük a Karácsony- és a Tarlós-vektor különbségének skaláris szorzatát a Puzsér-vektorral:
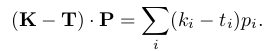
Itt is a koordinátageometriai emlékekre kell hivatkozni. Mint tudjuk, két vektor skalárszorzata a hosszúságaik (ezeket Pitagorasz-tétellel számoljuk) és a köztük levő szög koszínuszának szorzatával is egyenlő. Ebből és a fenti, koordinátás skalárszorzatból ki tudjuk számítani a koszínuszt, s abból a szöget.
Az eredmény az, hogy a fenti különbségvektorral a Puzsér-vektor kb. 93 fokos, a merőlegesnél egy kicsit nagyobb, „hátrahajló” szöget zár be, azaz tényleg egy kicsit, de nem igazán jelentősen több van benne a különbségben negatív T-ből, mint a pozitív K-ból.
Tényleg az eredmény
Tehát, ha átjárásról árulkodó hasonló mintázatot kell találni a Sétáló Budapest és a nagy politikai tömbök között, akkor a XI. kerületi adatok fényében erre nincs sok esély; s azon belül is az összellenzék felé való átjárás a valószínűtlenebb. A Sétáló Budapest semmit nem rontott a baloldali ellenzék esélyein. Kicsit hatásvadászabb módon megfogalmazva: a Sétáló Budapest indulása nélkül előfordulhatott volna, hogy ma a Fidesz egy leheletnyivel jobban állna. Alapvetően nem változott volna meg az eredmény, de esetleg egy kicsit erősebb lenne a kormánypárti ellenzék ebben a kerületben.
Ehhez persze – lássunk világosan! – szükség volt arra, hogy a Sétáló Budapest egyértelműen a mai ellenzékkel szemben is pozicionálta magát. Nyilvánvaló, hogy nem elég az ellenzéktől külön indulni, tényleg külön kell állni. Ha például a Momentum leszakadna az összefogásról, akkor – hiába próbál egy más minőséget megjeleníteni – valóban tőlük (is) szipkázna el szavazatokat. Fel kell fogni, hogy ma a hazai nem kormánypárti politikában nem valamilyen tartalmi kérdés, hanem az összefogás-nem összefogás a fő választóvonal; ki-ki tehát e mentén válasszon először, s a szervezeten belül megoldani, elrejteni próbált konfliktus helyett akár öncsonkítás árán tartsa meg tagsága egyetértését. Ez az, amit először Puzsér Róbert tett láthatóan ki az asztalra (az MKKP pedig „csak úgy”, a maga konstruktív természetességében műveli; az első tudatos példakövető pedig a Polgári Válasz). És persze ez az, amit a baloldal szeretne tagadni, hiszen a nem összefogós szavazatokat, ha nem ők, akkor ne tudja begyűjteni inkább senki más sem.